Algebra

Andres Haavasalu, Carl Robert Jakobsoni nimeline Gümnaasium, 2010

Algebrast üldiselt

Tehteid naturaalarvudega ja positiivsete ratsionaalarvudega osati juba kauges minevikus. Täisarvudega tehtavate aritmeetiliste tehete meetodid kujunesid välja Indias, sealt sai alguse arvude positsiooniline kümnendsüsteem. Esimesed kirjalikud andmed hindude aritmeetika kohta pärinevad VII sajandi keskpaigast. Tänapäeval kasutatavaid araabia numbreid võiks seega nimetada ka hindu numbriteks. Araablaste kaudu levisid hindu numbrid Euroopasse. Araabia matemaatiku al-Horazmi (u 780 – u 850) kaks ladina keelde tõlgitud teost avaldasid suurt mõju matemaatika arengule Euroopas. Neist ühe pealkiri oli „Aritmeetika hindu numbritega“, teise teose ladinakeelse tõlke pealkirjast „Algebra et Almucabala“ pärineb sõna „algebra“. Selles raamatus vaadeldi 1. ja 2. astme algebraliste võrrandite lahendamisele taanduvaid ülesandeid, samuti võrrandi ühelt poolelt teisele ülekandmise abil negatiivse arvu muutmist positiivseks. See teos kujunes algebraõpikute eelkäijaks Euroopas. Kuna tol ajal ei loetud negatiivseid arve tõelisteks arvudeks, siis tundus „algebra“ lausa imena. Algebrat nimetati suureks kunstiks, kusjuures väikese kunsti all mõeldi aritmeetikat. Terminit „algebra“ kui taastamiskunsti kasutasid araablased ka meditsiinis. Näiteks murtud luu kokkukasvatamine kuulus ju taastamiskunsti valdkonda. Algebra oli omapärane veel seetõttu, et ta lahendas üldkujul aritmeetika ülesandeid. Kuni XVI sajandini oli algebra käsitlus enamasti sõnaline. Tähelise sümboolika, tehtemärkide ja muude tähistuste kasutuselevõtt oli pikaajalise arengu tulemus. Klassikalise algebra põhiülesanne oli algebraliste võrrandite lahendamine. Algebrat on nimetatud ka võrrandite lahendamise kunstiks ning võrrandeid algebra keeleks. Alates XVII sajandist hakati tundmatuid suurusi tähistama ladina tähestiku tähtedega x, y ja z. Tänapäeva algebra on matemaatika osa, milles uuritakse operatsioone ja nende omadusi. Algebra etendab tähtsat osa matemaatikas endas ning leiab rakendusi teistes teadustes.

I kooliaste (1.- 3. klass)

Uue õppekava järgi leiab I kooliastmes õpilane võrduses tähe arvväärtuse proovimise või analoogia põhjal. Ei nõuta tähe arvväärtuse leidmist andmete ja otsitava vaheliste seoste kaudu. Tekstülesannete lahendamisel peab õpilane hindama tulemuste reaalsust.

1. klass

Esimese klassi õpilased on kooliks erineva ettevalmistusega, mis on tingitud mitmetest asjaoludest. Sellegi poolest on lastel ootusärevus ning tahe õppida. Kooliõpetuse kaudu hakkavad nad ümbritsevast maailmast paremini aru saama. Neil hakkab kujunema oma maailmapilt. Matemaatikal on selles protsessis küllalt suur osa. Näitlikustamine annab õpetamisel häid tulemusi. Piltidel ning looduses olevate lindude, loomade, puude, põõsaste, autode, majade jms. abil saab õpetada mõisteid pikem ja lühem, kõrgem ja madalam, laiem ja kitsam, paksem ja õhem, ülal ja all, ees ja taga, paremal ja vasakul, rohkem, vähem ja võrdselt, raskem ja kergem, kiirem ja aeglasem, soojem ja külmem, kallim ja odavam, kaugemal ja lähemal, suurem ja väiksem. Õpitakse arve 0-st kuni 100-ni lugema, kirjutama, võrdlema ja järjestama. Õpitakse paigutama naturaalarvude ritta sealt puuduvaid arve, määrama arvu asukohta naturaalarvude reas.

Näide. Kirjuta tärni asemele puuduv arv:

• 1 , ∗, 3 ;
• ∗ , 2, 3;
• ∗ , ∗,  3.

Näide. Kirjuta tärni asemele antud arvule vahetult eelnev ja vahetult järgnev arv:

• ∗ , 6, ∗ ;
• ∗ , 8, ∗ .

Õpitakse liitma ja lahutama 20 piires. Õpitakse märke +, −, =, >, < ja nende tähendust. Kui õpilased saavad aru liitmise ja lahutamise vahelisest seosest, tuleks pakkuda ülesandeid summas puuduva liidetava äraarvamise kohta.

Näide. Kirjuta tärni asemele selline arv, et võrdus kehtiks:

• ∗ + 7 = 9;
• 5 + ∗ = 8.

Järgmiseks sammuks võiks olla võrdusesse tähe sissetoomine.

Näide. Millise arvu saab panna tähe a asemele, et kehtiks võrdus 4 + a = 7 ?
Õpilane lahendab selliseid ülesandeid proovimise teel oma arvutusoskuse piires, kusjuures ei õpita reegleid tehete liikmete leidmiseks. Kui taoliste ülesannete lahendamine selgeks saab, võib õpilastele pakkuda tekstülesandeid 20 piires liitmise ja lahutamise kohta. Esialgu tuleb piirduda ühetehteliste ülesannetega.

Näide.

• Parkimisplatsil on 8 sõiduautot ja 6 veoautot. Mitu autot on parkimisplatsil?
• 12 õpilast mängis võrkpalli. Neist 7 olid tüdrukud. Mitu poissi mängis võrkpalli?

Saadud vastuste õigsust ja reaalsust peab kriitiliselt hindama. Õpilastele võib anda ka osalise tekstiga ülesandeid, et nad saaksid ise küsimusi esitada.

Näide. Mikk on 7-aastane. Rein on Mikust 5 aastat vanem. Mida saad arvutada? Koosta küsimus ja arvuta.

2. klass

Teises klassis õpitakse arve 0-st kuni 1000-ni lugema, kirjutama, järjestama ja võrdlema. Arvude võrdlemisel kasutatakse sümboleid >, <, = . Võrreldakse mitme liitmis- või lahutamistehtega arvavaldiste väärtusi. Õpitakse arvu suurendamist või vähendamist mingi arvu võrra. Õpilane liidab ja lahutab peast 20 piires, liidab peast ühekohalist arvu ühe- ja kahekohalise arvuga 100 piires, lahutab peast kahekohalisest arvust ühekohalist arvu, liidab ja lahutab täiskümneid ja – sadasid 1000 piires. Ei õpita reegleid tehete liikmete leidmiseks. Õpitakse arve 1 – 10 korrutama ja jagama 2, 3, 4 ja 5-ga. Jätkub esimeses klassis alustatud tähe arvväärtuse leidmine võrduses analoogia ja proovimise teel. Ülesannetes piirdutakse vaid võrdustega, mis sisaldavad ühte tehet ühe tähega.

Näide. Leia tähe arvväärtus, kui

• 23 + a = 30
• 34 + a = 43
• a + 8 = 50
• 2 ⋅ a = 10
• 3⋅ a = 27
• 4 ⋅ a = 24
• 5 ⋅ a = 35
• a : 2 = 3.

Ülesande 23 + a = 30 lahendamisel otsib õpilane proovimise teel sellist arvu, mida 23-le liites, saab tulemuseks 30. Vastus: a = 7 . Ülesande 34 + a = 43 lahendamisel võiks näha, et liites 34-le 6 , saadakse 40. Et saada 43, tuleb liita veel 3. Vastus: a = 9.
Jätkub ühetehteliste tekstülesannete lahendamine omandatud arvutusoskuse piires. Lisaks sellele õpitakse lahendama lihtsaid kahetehtelisi tekstülesandeid. Tekstülesannete lahendamine on igas kooliastmes raske. Siin on lugemisoskus seotud tekstist arusaamisega. Paljud õpilased lahendavad ülesande peast ja kirjutavad vihikusse vaid vastuse. Peastlahendamise oskus on tervitatav, kuid ka lahenduskäigu kirjapanemist kui vajalikku oskust tuleb õpetada.

Näide. Ühes klassiruumis on 14 arvutit, teises klassiruumis on arvuteid 6 võrra rohkem. Mitu arvutit on kahes klassiruumis kokku?

3. klass

Kolmandas klassis õpitakse arve 0-st kuni 10000-ni lugema, kirjutama, järjestama ja võrdlema. Peast arvutatakse vaid 100 piires, suuremate arvude korral arvutatakse kirjalikult. Korrutustabel tuleb selgeks saada. Õpitakse mõisteid „korda suurem“ ja „korda väiksem“. Korrutatakse peast ühekohalist arvu kahekohalise arvuga, jagatakse peast kahekohalist arvu ühekohalise arvuga. Jätkub tähe arvväärtuse leidmine võrduses analoogia ja proovimise teel. Piirdutakse vaid võrdustega, mis sisaldavad ühte tehet ühe tähega. Soovitav on kasutada ülesannetes erinevaid tähti.

Näide. Leia tähe arvväärtus, kui

• a + 9 = 60
• b + 7 = 20
• 24 + m = 32
• 2 ⋅ k = 10
• t ⋅3 = 27
• 6 : s = 3
• 12 : u = 4
• d : 2 = 3.

Ülesande 2 ⋅ k = 10 lahendamisel otsib õpilane proovimise teel sellist arvu, mis 2-ga korrutamisel annab tulemuseks 10. Vastus: k = 5.
Õpilane määrab avaldises tehete järjekorra (sulud, korrutamine, jagamine, liitmine ja lahutamine). Õpitakse summa korrutamist ja jagamist arvuga. Lahendatakse ühe- ja kahetehtelisi tekstülesandeid õpitud arvutusoskuse piires. Lisandub ühetehteliste tekstülesannete koostamine, mille abil arendatakse eneseväljendamise oskust. Õpilane esitab ülesande lahendamiseks vajalikud küsimused, seejärel arvutab ning hindab saadud tulemuste reaalsust.

Näide. Aias kasvab 2 meetri kõrgune õunapuu. Maja on 6 meetri kõrgune.Võrdle õunapuu ja maja kõrgust. Koosta nende andmete põhjal küsimus ning arvuta.
Mitme meetri võrra on maja kõrgem kui õunapuu? Lahendus: 6 − 2 = 4 (m).
Vastus: maja on 4 meetri võrra kõrgem kui õunapuu.
Mitu korda on maja kõrgem kui õunapuu? Lahendus: 6 : 2 = 3.
Vastus: maja on kolm korda kõrgem kui õunapuu.

II kooliaste (4.- 6. klass)

4. klass

Neljanda klassi õpilane loeb ja kirjutab, võrdleb ja järjestab, liidab ja lahutab arve 1 000 000 piires, nimetab arvule eelneva või järgneva arvu, kujutab arve arvkiirel. Liidab ja lahutab peast kuni kolmekohalisi arve. Sõnastab ja kirjutab üldkujul liitmise ja korrutamise omadusi (vahetuvus, rühmitamine, summa korrutamine arvuga). Esmalt võiks teha tehteid arvudega kuni 10 000-ni ja seejärel suuremate arvudega. Õpilane tunneb tehete järjekorda nii sulgudeta kui ka ühe paari sulgudega arvavaldises. Arvutab kahe- ja kolmetehtelise arvavaldise väärtuse. Leiab ühetehtelises võrduses tähe arvväärtuse proovimise või analoogia teel. Piirdutakse vaid võrdustega, milles on üks tehe ühe tähega.

Näide. Leia tähe arvväärtus, kui b + 24 = 37 .
Õpilane otsib proovimise teel sellist arvu, millele 24 liitmisel, saadakse tulemuseks 37. Vastus: b = 13 .
Õpilane lahendab kuni kahetehtelisi tekstülesandeid.

Näide. Viljahoidlast veeti rongiga ära 1620 tonni vilja. Kui pikk oli rong, kui ühte vagunisse mahub 60 tonni vilja ning vaguni pikkus on 25 meetrit?
Lahendus. Mitu vagunit läks vaja? 1620 : 60 = 27 vagunit.
Kui pikk oli rong? 27 ⋅ 25 = 675 (m).
Vastus: rongi pikkus oli 675 meetrit.
Õpilane koostab ühetehtelisi tekstülesandeid.

Näide. Esmaspäeval müüs kauplus 380 liitrit piima, teisipäeval aga 90 liitri võrra rohkem. Esita küsimus ja arvuta.
Mitu liitrit piima müüs kauplus teisipäeval? 380 + 90 = 470 (l).
Vastus. kauplus müüs teisipäeval 470 liitrit piima.

5. klass

Viiendas klassis õpitakse miljardi piires naturaalarve kirjalikult liitma ja lahutama, korrutama kirjalikult kuni kolmekohalisi naturaalarve, jagama kirjalikult kuni 5-kohalisi naturaalarve kuni 2-kohalise naturaalarvuga. Õpitakse määrama tehete järjekorda liitmise, lahutamise, korrutamise, jagamise ja sulgude suhtes ning rakendama neid oskusi kuni neljatehtelise arvavaldise väärtuse arvutamisel. Õpitakse ka kümnendmurde ja tehteid nendega, samuti mõõtühikuid. Liidetakse, lahutatakse ja korrutatakse nimega ning nimeta arve.

Näide. Leia vastus sentimeetrites: 5,8m + 0,47m .
Lahendus. 5,8m + 0,47m = 6,27m = 627cm.
Õpilane teeb vahet arvavaldisel, tähtavaldisel ja valemil, lihtsustab ühe muutujaga täisarvuliste kordajatega avaldist. 

Näide. Lihtsusta avaldis

• 18m + 53m − 6m ;
• 21a −13a + 32a .

Avaldise lihtsustamist saab siduda ka õpitud geomeetriliste kujunditega ning igapäevaeluga.

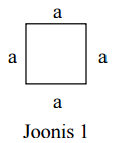
Näide. Toa põrand on ruudukujuline, mille külje pikkus on a (vt joonis 1). Avalda põranda ümbermõõt.

Ümbermõõdu avaldist saab esitada mitmel viisil: a + a + a + a või 4a . Kui tähistada ümbermõõt tähega P, siis P = 4a on valem ruudu ümbermõõdu leidmiseks. Viiendas klassis tuuakse sisse võrrandi mõiste. Õpitakse võrrandit, mis sisaldab ühte tundmatut, ühte tehet ning naturaalarve. Võrrand lahendatakse proovimise ja analoogia teel. Õpitakse ka võrrandi lahendit kontrollima.

Näide. Lahenda võrrand 350 + x = 620 . Millise arvu peame liitma arvule 350, et saada 620 ? Proovimise teel saadakse vastuseks 270. See ongi võrrandi lahend. Lahendi kontrollimiseks asendame x arvuga 270 ja veendume, et saame tõese võrduse. Õpilane lahendab kuni kahetehtelisi tekstülesandeid.

6. klass

Kuuendas klassis õpitakse protsendi mõistet. Teatakse, et protsent on üks sajandik tervikust. Järgnevalt käsitletakse vaid protsentides antud osa leidmist tervikust (ka intressiarvutusi). Kõik muu protsendiga seonduv on uue RÕK järgi viidud seitsmendasse klassi. Õpitakse negatiivseid arve ning saadakse teada, et negatiivsed täisarvud koos naturaalarvudega ning arvuga null moodustavad täisarvude hulga. Pole kindlat seisukohta, kas null on naturaalarv või mitte. Õpilane arvutab kirjalikult täisarvudega, lahendab kuni kahetehtelisi tekstülesandeid täis- ja murdarvudega. Arvutab ühetähelise tähtavaldise väärtuse, koostab ise lihtsaid tähtavaldisi, näiteks pindala ja ruumala leidmise kohta.

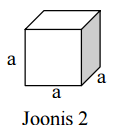
Näide. Kuubi serv on a. Koosta avaldised kuubi pindala ning kuubi ruumala leidmiseks ( vt joonis 2).

Tähelepanu tuleb pöörata tehetele harilike murdudega. Siin pannakse alus oskusele, mida läheb hiljem vaja algebraliste murdudega opereerimisel, ratsionaalavaldiste teisendamisel ning võrrandite lahendamisel. Kui osatakse tehteid harilike murdudega, siis on tehted algebraliste murdudega kergemini omandatavad.

III kooliaste (7.- 9. klass)

7. klass

Uue õppekava järgi on sisse toodud mõisted promill ja protsendipunkt, mida käsitletakse tutvustavalt. Promilli kasutamist selgitatakse eluliste näidete abil (alkoholi sisaldus veres, soola sisaldus merevees, toimeaine hulk ravimis). Õpitakse terviku leidmist protsentides antud osamäära järgi, kahe arvu suhet protsentides, suuruse kasvamise ja kahanemise väljendamist protsentides. Õpilane eristab muutust protsentides muutusest protsendipunktides. Põhikoolis ei õpetata negatiivset astendajat, välja arvatud arvu 10 negatiivse täisarvulise astendajaga aste. Ei õpetata võrratusi, samuti tekstülesandeid pöördvõrdelise sõltuvuse kohta. Seitsmendas klassis õpitakse naturaalarvulise astendajaga astet, arvu 10 astmeid ning kirjutama suuri arve kümne astmete abil. See on vajalik arvu esitamiseks standardkujul.

Näide. Päikese kaugus maast on ligikaudu 150 000 000 km ehk 150 000 000 000 m. Sellise tülika arvu saab kirjutada lühemalt 1,5⋅10¹¹ m .

Näide.

• 1 cm = 0,01 m = 10^-2 m
• 5 g = 0,005 kg  = 5 ⋅ 10^-3 kg .
  Õpilane astendab negatiivset arvu naturaalarvuga ning teab sulgude tähendust. Viimase rõhutamine on eriti oluline.

Näide.

• -3² = -9
•  (-3)² = 9

Võrrand

Seitsmendas klassis alustatakse tõsisemalt võrrandi õppimist. Õpitakse võrrandite samaväärsust ja võrrandi põhiomadusi. Õpilane lahendab ühe tundmatuga lineaarvõrrandit.

Näide. Lahenda võrrand 4x + 2 = 3x + 5 .

Võrrandi liikmeid võib viia võrrandi ühelt poolelt teisele poolele vastandmärgiga. Viime tundmatuga liikmed võrrandi vasakule poolele ning vabaliikmed paremale poolele. Saame 4x − 3x = 5 − 2 ning lahendiks on x = 3 . Kontrollime lahendit. Kontrollida tuleb esialgset võrrandit. Asetame võrrandis x asemele 3. Saame vp = 4 ⋅ 3 + 2 = 14 ning pp = 3 ⋅ 3 + 5 = 14.
Näeme, et vp = pp . Arv 3 rahuldab võrrandit. Vastus. x = 3 .

Näide. Lahenda võrrand 2(4x + 5) = 6x + 12. Avame sulud ning seejärel toimime analoogiliselt eelmise näitega. Saame 8x +10 = 6x +12 Seejärel 8x − 6x = 12 −10 , 2x = 2 . Jagades võrrandi mõlemat poolt 2-ga , saame x = 1.
Kontrollime lahendit: vp = 2(4 ⋅1+ 5) = 2 ⋅9 = 18 ; pp = 6 ⋅1+12 = 18 ; vp = pp . Vastus: x = 1.

Õpilane lahendab võrdekujulist võrrandit.

Näide. Lahenda võrrand ^3x⁄₄ = ³⁄₂ .

Võrde põhiomaduse põhjal: 6x = 12 , millest x = 2 . Kontroll: vp = pp = ³⁄₂. Vastus: x = 2 .

Näide. Lahenda võrrand ³²⁄_m = 8. Selle võrrandi võime kirjutada kujul ³²⁄_m = ⁸⁄₁. Analoogiliselt eelmise näitega: 8m = 32 ning m = 4 . Kontroll: 8 vp = pp = . Vastus: m = 4 .

Näide. Lahenda võrrand ^{3x + 2}⁄₂ = x + 4

Ka selle võrrandi võime kirjutada kujul ^{3x + 2}⁄₂ = ^{x + 4}⁄₁. Võrde põhiomaduse põhjal: 3x + 2 = 2(x + 4) ; 3x + 2 = 2x + 8 ; 3x − 2x = 8 − 2 , millest x = 6. Kontroll: vp = ^{3 ⋅ 6 + 2}⁄₂ = ²⁰⁄₂ = 10 ; pp = 6 + 4 = 10 ; vp = pp . Vastus: x = 6.

Tähelepanu tuleb pöörata võrdest ühe liikme avaldamisele. Tuleb kasutada ka x-st erinevaid tähti, et õpilane tunneks võrde ära mõne teise aine õppimisel ja mistahes tähe korral. Võrdekujulise võrrandi lahendamisoskus on oluline füüsikas ja keemias.

Õpilane lahendab lihtsamaid, sealhulgas igapäevaeluga seonduvaid tekstülesandeid võrrandi abil. Ta saab aru, et võrrand aitab lahendada tekstülesannet.

Näide. Aias on kirsipuid 4 korda rohkem kui ploomipuid. Mitu kirsipuud ja ploomipuud on aias, kui kokku on 20 viljapuud?
Lahendus. Tähistame ploomipuude arvu x-ga. Kirsipuude arv on siis 4x . Kuna kokku on viljapuid 20, saame võrrandi 4x + x = 20 . Sellest 5x = 20 ning x = 4 . Ploomipuid on 4 ning kirsipuid 4 ⋅ 4 = 16 . Kontroll tuleb teha ülesande teksti põhjal. Kokku on viljapuid 4 +16 = 20 . Vastus: aias on 16 kirsipuud ning 4 ploomipuud.

Mõne ülesande lahenduse puhul piisab vastuse nägemisest, et öelda: vastus pole õige (näiteks, kui suusataja kiirus on 120 km / h).

Võrrandi koostamist võib siduda õpitud geomeetriliste kujunditega. Saab rõhutada, et võrrand pole mitte tüliks, vaid on vahendiks geomeetriaülesande lahendamisel.

Näide. Kasutades joonisel 3 olevaid andmeid, leia kolmnurga külgede pikkused, kui kolmnurga ümbermõõt on 54 cm. Koosta võrrand kolmnurga külgede pikkuste leidmiseks ning lahenda see võrrand.

Üksliikmed

Uue õppekava järgi õpetatakse üksliikmeid seitsmendas klassis (varem kaheksandas klassis). Õpilane teab, mis on üksliikme kordaja. Teab, et kordaja 1 jäetakse kirjutamata ning miinusmärk üksliikme ees tähendab kordajat -1. Õpitakse võrdsete alustega astmete korrutamist ja jagamist, korrutise ja jagatise astendamist, astme astendamist. Omandatakse järgmised valemid: a^m ⋅ aⁿ = a^{m + n}, a^m : aⁿ = a^{m – n} (seda eeskirja kasutatakse esialgu vaid juhul, kui m > n , sest õpilased ei tunne veel negatiivse astendajaga astet ega ka astet astendajaga 0), (ab)ⁿ = aⁿ ⋅ bⁿ , (^a/_b)ⁿ = ^an/_bⁿ , (a^m)ⁿ = a^mn. Õpitakse üksliikmeid liitma ja lahutama, korrutama ja jagama ning koondama. Õpilane viib üksliikme normaalkujule ning määrab üksliikme kordaja.

Näide. Kirjuta üksliige ²/₅aab ⋅ ³/₄aaabb normaalkujul ja määra selle kordaja.

8. klass

Hulkliikmed

Uue õppekava järgi pole õpitulemustes kuupide summa ja kuupide vahe ning kaksliikme kuubi valemeid. Need tuuakse sisse (õpiku B osa) ülesannetes, mis sobivad lahendamiseks tugevamatele õpilastele. Õpilane tegurdab hulkliiget ühise teguri sulgudest väljatoomise ja valemite rakendamisega. Õpilane teab mõisteid kaksliige, kolmliige, hulkliige ning nende kordajaid, korrastab hulkliiget, arvutab hulkliikme väärtuse. Õpilane liidab ja lahutab hulkliikmeid, korrutab ja jagab hulkliiget üksliikmega, korrutab hulkliiget hulkliikmega (piirdutakse juhtumiga, kus kolmliiget on vaja korrutada kolmliikmega).

Näide. 1. Koonda ja korrasta hulkliige 7x²y + 5x – 4xy – 2x .
Lahendus. 7x²y + 5x – 4xy – 2x = 7x²y – 4xy + 3x .

2. Arvuta avaldise 4ab + 2ab − 3ab väärtus, kui a = 5 ja b = -6 .
Lahendus. 4 ⋅ 5 ⋅ (−6) + 2 ⋅ 5 ⋅ (−6) − 3 ⋅ 5 ⋅ (−6) = −120 − 60 + 90 = −90

3. Lihtsusta avaldis (3m + 5) + (7m − 2) − (4m − 3) .
Lahendus. (3m + 5) + (7m − 2) − (4m − 3) = 3m + 5 + 7m − 2 − 4m + 3 = 6m + 6.

4. Korruta üksliige hulkliikmega ¹/₄x(8x² – 12x + 3) .
Lahendus. ¹/₄x(8x² – 12x + 3) = ¹/₄ ⋅ 8 ⋅ x ⋅ x² – ¹/₄ ⋅ 12 ⋅ x ⋅ x + ¹/₄ ⋅ 3 ⋅ x = 2x³ – 3x² + ³/₄x

5. Jaga hulkliige üksliikmega (12m²n – 15mn + 18m) : 3m .
Lahendus. (12m²n – 15mn + 18m) : 3m = 4mn – 5n + 6 .

6. Korruta kolmliige kaksliikmega ) (x² + 6x + 5)(2x – 3) .
Lahendus. (x² + 6x + 5)(2x – 3) = 2x³ – 3x² + 12x² – 18² + 10x – 15 = 2x³ + 9x² – 8x – 15 .

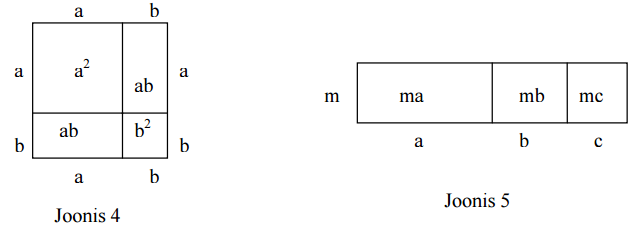
Õpitakse kahe üksliikme summa ruudu valemit (a + b)² = a² + 2ab + b² , kahe üksliikme vahe ruudu valemit (a − b)² = a² − 2ab + b² ja kahe üksliikme ruutude vahe valemit a² − b² = (a + b)(a − b). Nende valemite abil on võimalik arvutamist lihtsustada. Esimest kahte valemit on sobiv geomeetriliselt illustreerida (vt joonis 4). Kui a ja b on positiivsed arvud, siis avaldisi (a + b)² ja (a − b)² (kus a > b) võib vaadelda ruutude pindaladena. Jooniselt 4 on näha, et ruudu külg on a + b ning selle ruudu pindala (a + b)² on võrdne kahe ristküliku pindala ning ühe ruudu pindala summaga. Analoogiliselt saab illustreerida ka vahe ruudu valemit. Lisaks kaksliikme summa ja vahe ruudu valemitele tuleks näidata, et kehtivad järgmised seosed:

(a – b)² = [-(a + b)]² = (-1)²(a + b)² = (a + b)²

(a – b)² = a² – 2ab + b² = b² – 2ab + a² = (b – a)² ja (-a + b)² = (b – a)²

Hulkliikme tegurdamist ühise teguri sulgudest väljatoomisega võib ka geomeetriliselt näitlikustada.

Näide. Tegurda ma + mb + mc = m(a + b + c). Jooniselt 5 on näha, et kolme väikese ristküliku pindalade summa on ma + mb + mc ning see on võrdne suure ristküliku pindalaga m(a + b + c) .

Näide. 1. Rakenda kaksliikme kuubi valemit: (a + 1)³ ja (m – 2)³.
Lahendus. (a + 1)³ = a³ + 3a² + 3a + 1;
(m – 2)³ = m³ – 6m² + 12m – 8 .

2. Tegurda x² – 8 ja t² + 27 .
Lahendus. x³ – 8 = (x-2)(x² + 2x + 4)
t³ + 27 = (t + 3)(t² – 3t + 9) .

3. Korruta (2m + 1)(4m² – 2m + 1) .
Lahendus. (2m + 1)(4m² – 2m + 1) = (2m)³ + 1³ = 8m³ + 1

Oluline on rõhutada, et õppematerjali miinimum tuleb selgeks õpetada lihtsate ülesannete abil. Pärast seda saab lahendada raskemaid ülesandeid, teisendades algebralisi avaldisi, kus tuleb kasutada kõiki õpitud valemeid. Kõik valemid ei pea olema korraga ühes ülesandes. Algebralise avaldise teisendamise oskus on vajalik, kuna seda läheb edaspidi vaja paljude kaheksanda klassi teemade õppimisel, aga ka järgmistes klassides.

Kahe tundmatuga lineaarvõrrandisüsteem

Kahe tundmatuga lineaarvõrrandis on pärast lihtsustamist üldjuhul kolm liiget: esimese tundmatuga lineaarliige, teise tundmatuga lineaarliige ja vabaliige, st 0 ax + by + c = . See on kahe tundmatuga lineaarvõrrandi normaalkuju, kus x ja y on tundmatud, a ja b on tundmatute kordajad ning c vabaliige. Kahe tundmatuga lineaarvõrrandil on üldiselt lõpmata palju lahendeid. Selle võrrandi graafiliseks kujutiseks on sirge. Seepärast nimetatakse võrrandit ax + by + c = 0 sirge võrrandiks. Õpilased õpivad lahendama kahe tundmatuga lineaarvõrrandisüsteemi. Võrrandisüsteemi lahenditeks on mõlema võrrandi ühised lahendid. Õpitakse liitmisvõtet, asendusvõtet ja graafilist lahendamist.